How To Draw A Polar Plot For Mud Weight
Abstract
The challenges behind this research were encountered while drilling into the Ilam, Mauddud, Gurpi, and Mishrif Formations, where astringent drilling instability-related issues were observed across the weaker formations in a higher place the reservoir intervals. In this paper, geomechanical parameters were carried out to determine optimum mud weight windows and safe drilling deviation trajectories using the geomechanical parameters. We advise a workflow to determine the equivalent mud window (EMW) that resulted in 11.eighteen–12.61 ppg which is suitable for Gurpi formation and 9.36–13.13 ppg for Ilam and Mishrif Formations, respectively. To estimate condom drilling trajectories, the Poisson's ratio, Young's modulus, and unconfined compressive forcefulness (UCS) parameters were determined. These parameters illustrate an optimum drilling trajectory bending of 45° (Azimuth 277°) for the Ilam to Mauddud Formations and less than 35° for the Gurpi Formation. Our analysis reveals that maximum horizontal stress and Poisson'southward ratio have the about impact on determining the optimum drilling mud weight windows and safe drilling divergence trajectories. On the opposite, vertical stress and Young's modulus have minimum touch on on drilling mud weight windows and condom drilling departure trajectories. This study can be used every bit a reference for the optimal mud weight window to overcome drilling instability issues in futurity wellbore planning in the study.
Introduction
A question that may come into the readers' mind is: why does the determination of the geomechanical parameters have the most affect on decreasing risks during wellbore operation, and why this written report is focused on the Ilam, Mauddud, Gurpi, and Mishrif formations. The respond is that generally, the breakout happens effectually the wellbore at the same orientation as the minimum principal stress, with a high-stress concentration. Therefore, the borehole enlargement happens when drilling fluid density is less than the strength of the rocks. Thus, shear failure happens at a low drilling fluid density, while the tangential stress is high. On the other hand, the Ilam, Mauddud, Gurpi, and Mishrif formations consist of argillaceous limestone and marl with scattered asphalt, with the salt aquifer. Therefore, the estimation of the geomechanical parameters is necessary to be adamant and implemented to reduce the drilling risks during operation. Another question that may come into the readers' minds is: what is the novelty of this inquiry? The reply is that the novelty of this research refers to the determination of the mud weight window, optimum drilling trajectory, and wellbore stability, including new observations which lead to new results in the study area.
The geomechanical parameter estimation is frequently used to forestall lost apportionment and the determination of optimum drilling trajectory. To make up one's mind the safe mud weight window and the best drilling trajectory, information technology is required to determine the intervals of tensile rock failure and shear rock failure. The pressure of the drilling mud will cause a tensile failure in the wellbore, and drilling mud will be lost into the germination if the mud weight is applied college than the safety mud window. Shear failure or breakout will occur while this weight is applied lower than the safe mud window (Le and Rasouli 2012; Zhang 2013; Zoback et al. 2003). Tensile stone failure occurs in the upper meters near the surface, while shear rock failure takes place at greater depth, below which, rock failure does not occur. Parameters such as wellbore deviation and principal stress directions play a remarkable role in calculating the mud weight window. Principal stresses directions are important to be quantified for petroleum field development (Radwan 2021a). Geomechanical modeling, wellbore stability analysis, and associated parameters have been examined in many research in recent years. Radwan et al. investigated pore force per unit area and fracture gradients using a variety of data and methods (Radwan et al. 2019, 2020, 2021). They also carried out reservoir geomechanical modeling in lodge to analyze in situ stress and its human relationship with reservoir backdrop such equally depletion, product, and wellbore stability (Radwan and Sen 2021a, 2021b; Radwan et al. 2021). To improve nether-balanced drilling, Abdelghany et al. practical the depth-of-damage method in geomechanical modeling (Abdelghany et al. 2021). Kassem et al. (2021) calculated the geomechanical parameters to investigate the effect of depletion and fluid injection in a sandstone reservoir (Kassem et al. 2021). Shahbazi et al. (2020) investigated the impact of reduced production rates on wellbore stresses by amalgam a second geomechanical model using log data and drilling data in two Iranian oil fields.
Optimization of mud weight window is the most critical factor to forbid wellbore instability during directional drilling. An optimum mud weight window entails wellbore stability (Li and Zhang 2011) and prevents lost apportionment.
Before drilling, the stress on the ground is less than the force of the rocks and thus the balance of the ground is retained. Just both during and afterwards the drilling, function of the rock column is drilled and moved out of the well, and the drilling mud replaces that and puts pressure on the wellbore wall, thus spreading stress around the wellbore, and the balance of stress in the basis is disrupted and the stress generated past the drilling is created. To maintain wellbore stability and regulate these stresses, the well must be drilled with the advisable mud weight (Darvishpour et al. 2019). Failure to pay attention to this issue causes wellbore instability and problems such as collapse, kick, wash-out, or tighten, increasing drilling costs, stopping production, and eventually might indeed cause well loss (Das and Chatterjee 2017).
To determine wellbore stresses, the rock strength must be known, an appropriate model must exist selected, and an advisable stone failure benchmark should exist called. Rock strength is an essential parameter in wellbore stability considering it shows the behavior of the stone when information technology is under in situ stress conditions (Radwan 2021a, b, c). The rock strength properties can exist obtained from well logs data and empirical equations (Peng et al., 2001; Rahimi 2014).
Heller and Zoback (2014) provided 28 relationships by different researchers for estimating the unconfined compressive force (sandstones or carbonate rocks and shale). In virtually of these relationships, the chief variables are transit time of sonic waves, ultrasonic wave velocity, Young's modulus, and porosity.
In situ stresses, which are carried out in various methods, have been published by Radwan et al. (2021a, b, and c). The International Social club of Rock Mechanics suggests "hydraulic fracturing" as the about reliable arroyo to determine in situ stress. This technology can increase the product of a well, and the proper use of this method can improve reservoir permeability and consequently improve the product of the wells (Gao et al. 2019a, b, c; Kassem et al. 2021; Radwan et al. 2021d).
In this research, we carried out an optimum mud weight estimation using geomechanical parameters in two steps. Consequently, we propose a drilling deviation survey based on the geomechanical models.
Geological setting
The written report area is located in the Persian Gulf. The Persian Gulf Basin is considered the richest region in the globe in terms of hydrocarbon resources (Ghazban 2007). The studied reservoir in this oil field is referred to as Sarvak Formation.
The Mesozoic stratigraphy of the Persian Gulf basin is characterized past episodic development of intra-shelf basins over the northeastern margin of the Arabian plate (Sharland et al. 2001; Van Buchem et al. 2011). During Aptian and Cenomanian, these basins resulted in deposition of organic-rich sediments which adjoined porous rim carbonates on their margins (Vahrenkamp et al. 2015). The Cenomanian intra-shelf basin was adult following the deposition of the lower parts of the Sarvak Germination, which are regionally continuous and dominated by carbonates (Razin et al. 2010). These carbonates are overlain in the west and e by shallow-marine carbonates of the Mishrif platform rimming an NE-SW trending intra-shelf basin in the key parts of the study area (Vahrenkamp et al. 2015). Recent seismic studies in the Iranian sectors of the prolific Persian Gulf region (OEOC 2014) have resulted in numerous oil and gas discoveries within the Cretaceous Serial. The Middle Sarvak Formation (Cenomanian) is considered to be an of import source rock inside the Cretaceous petroleum system of the eastern Persian Gulf basin (Alipour 2017; Hosseiny et al. 2016). This source stone is suggested to accuse the overlying Mishrif and Ilam carbonates in some oilfields of the report surface area (Alipour et al. 2017; Alizadeh et al. 2017; Hosseiny et al. 2017).
Sarvak formation is function of the Bangestan Grouping, containing a neritic carbonate consisting of limestone and dolomite, and this formation has shallow and deep facies. The lower office of the Sarvak Formation consists of limestone and pelagic stone. The upper role includes massive limestone containing algae, echinoderms, and rudists (James and Wynd 1965; Ghazban 2007). The Sarvak Formation is derived from Tange Savrak in the mount Bnatsegnan (northwest of Behbahan Urban center) in Khuzestan Province (James and Wynd 1965; Rahimi and Riahi 2020). The Sarvak Formation in stratigraphical terms is equivalent to Khatiyah, Mauddud, Ahmadi, and Mishrif Formations in this area (Ghazban 2007). The Upper Sarvak Germination is equivalent to the Mishrif Formation deposited in the south part of the Persian Gulf. This formation is regarded equally a significant hydrocarbon reservoir of this area (Van Buchem et al. 1996; Rahimi and Riahi 2020). The lower part of Mishrif is Khatiyah Formation that consists of organic matter-rich mudstone and wackestone. The Mauddud Germination with Albian–Cenomanian historic period consists of a shallow-water carbonate with widespread distribution in the Persian Gulf. The Mauddud Formation is a carbonate-dominated succession that emerged from transgression afterward the Nahr Umr Formation-related clastic-dominated sediments in the Western farsi Gulf (James and Wynd 1965) Fig. one.
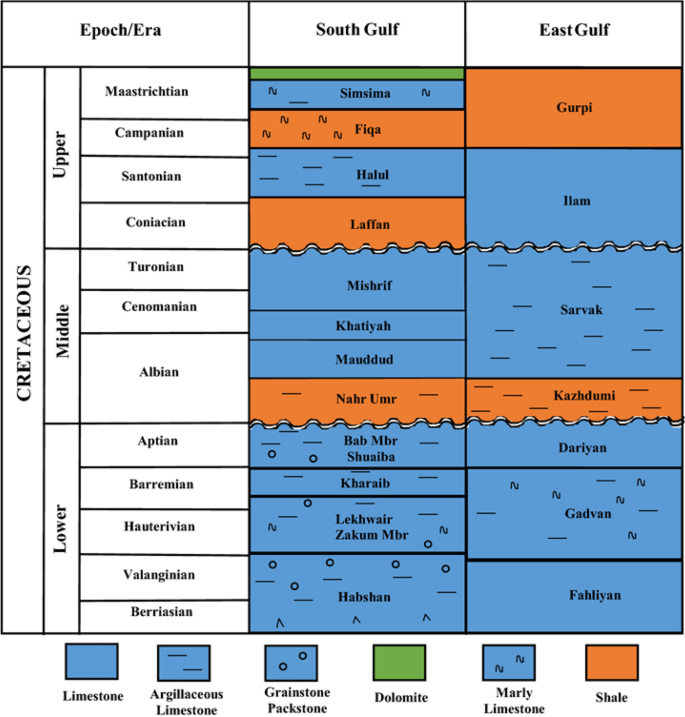
Cretaceous stratigraphy chart of the Western farsi Gulf (Rahimi and Riahi 2020)
Petrophysical backdrop
Petrophysical parameters such as effective and full porosity, water saturation, shale volume, and volume of minerals in this reservoir were calculated using probabilistic assay. Just get-go, the mineralogy composition was determined. Iii lithology cross-plots for the Ilam, Mauddud, Mishrif, and Khatiyah formations, based on neutron vs. density and sonic vs. Vp/Vs logs, were performed. The average shale book calculated for the studied formations is near 2.6%, which indicates that these formations are composed by and large of limestone and calcite. Since the velocity of sonic waves varies according to the textile and lithology of the formation, shale, limestone, and dolomite are easily distinguishable. According to the bachelor sonic log, the lithology of the studied formations is made of calcite and limestone with a few corporeality of shale.
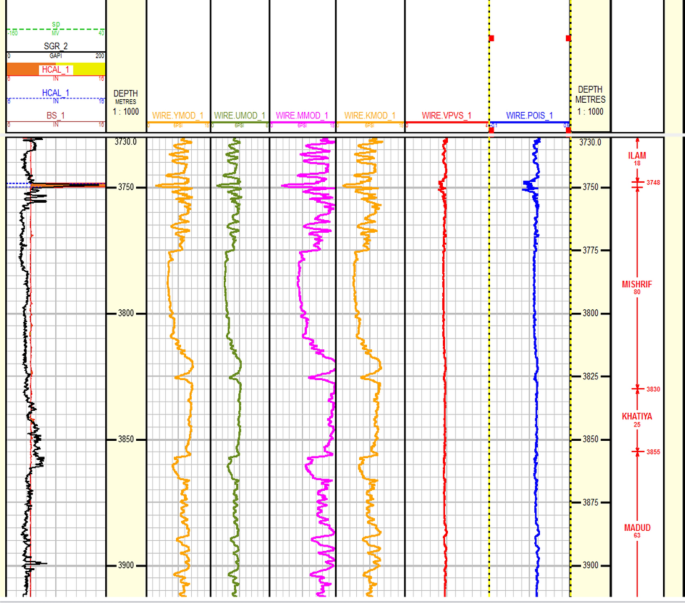
In the next pace, neutron density logs are used every bit a basis for depth matching of other logs, similar compensated gamma ray (CGR), thermal neutron (CNL/TNPHI) porosity, compressional slowness (DTCO), photoelectric factor (PeF), and resistivity from the wellbores (HE-E1 and HE-E2). These logs were employed to perform the petrophysical model. The petrophysical evaluation results (Fig. two) propose a carbonate reservoir with limited shale volume (2.6%) and a porosity average of 10%. Figure ii shows the volume of water saturation in the 2d track and the volume of minerals in the 3rd track, both from the right side.

Petrophysical logs of the hydrocarbon zones in the intervals of the Ilam, Mauddud, Mishrif, and Khatiya formations. This figure represents the petrophysical backdrop of the studied formations
In tracks 1 and ii, the corporeality of water saturation and porosity is observed from the right, respectively. At the depth of 3750 m, low porosity is evident in the shaly interval and an increment in water saturation is observed. In tracks 6 and seven from the right, according to the PEF log, the presence of limestone tin be seen throughout the depths interval of the wellbore. The PeF log shows a value of well-nigh 5, representing the presence of limestone but decreases at a depth of 3750 g. The decrement of the PeF value proves the existence of the inter-shaly layer. On the other hand, the electrical resistivity log value increases at a depth of 3750 m. The density and neutron logs (tracks 6 and 7) decrease at a depth of 3750 1000, representing the shaly interval. The conventional well logs that were employed in the petrophysical model were displayed in the other column of Fig. two. It is worth mentioning that the shale volume was calculated using a corrected gamma-ray log (SGR).
Materials and methods
Wireline logs consisting of compressional density, gamma ray, resistivity, FMI log (rose diagram), petrophysical evaluation results, and pore pressure points from MDT tools are the available data in this analysis. Based on the log data coverage in the entire well likewise equally the availability of direct downhole measurements, we have advisedly chosen one well, namely HE-E2 for the geomechanical analysis presented here. Drilling and well reports were studied and used in this work. Applied methods are discussed below.
Wellbore stresses and pore pressure (pp)
Unremarkably, in situ stress is divided into three parts: vertical stress, minimum horizontal stress, and maximum horizontal stress. The germination rocks are in forepart of the field stresses before drilling, but after drilling these rocks are pushed out in the cutting form and the wellbore must withstand the stresses of the field. These stresses relate to the wellbore trajectory besides as the impact of the field dominant stress on the well-drilling location (Nelson et al. 2006).
Maximum and minimum horizontal stresses
The minimum and maximum horizontal stresses are two of the three major stresses required for each geomechanical study (wellbore stability analysis, sand production, and hydraulic fracture) (Shmin and Shmax). Estimation of horizontal stresses is one of the chief steps in geomechanical modeling and contributes to an cess of the accuracy of the measured geomechanical model (Gholilou et al. 2017). The stresses applied to the rocks underground are nigh identical in various directions nether isotropic conditions and before well drilling (S5 = Shmin = Shmax). Still, these values change after drilling and these changes are more noticeable on a significant regional scale in active tectonic areas such equally anticlines, fault-side by side areas, salt domes, and other active tectonic areas. Mechanical failures in the wellbore are induced by adjusting the horizontal stress values. These mechanical failures can exist in the maximum horizontal stress direction in the course of tensile failures or breakdown, and shear failures or breakouts are in the minimum horizontal stress direction which both are produced roughly parallel to the wellbore centric. Using acoustic and density logs, as well as reservoir properties similar Poisson's ratio, vertical stress, and pore force per unit area, the stress contour in the reservoir is determined (Almalikee and Al-Najim 2018). At that place are many methods to assess the direction and location of these stresses. Image logs are i of the near detailed methods to classify the features of these stresses. Figure 3 shows the location and direction of breakouts created by shear stress observed on the rose diagram.
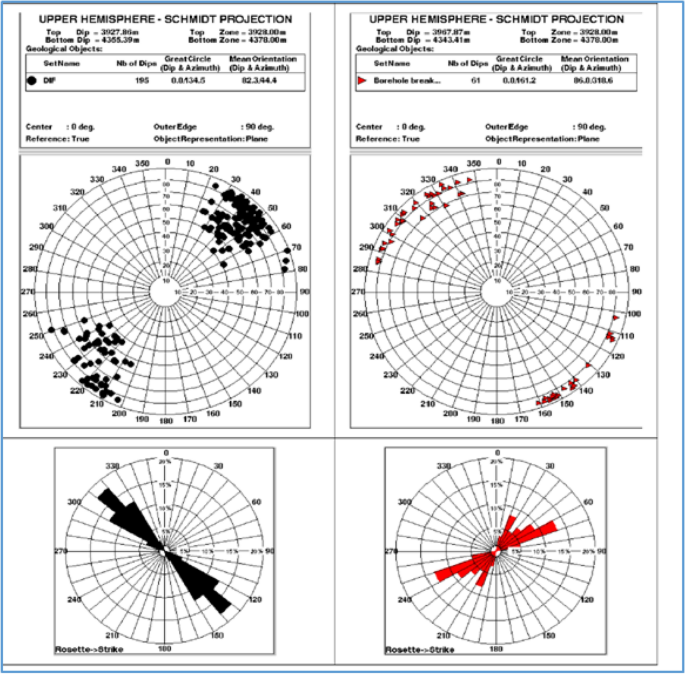
The FMI results showing that the direction of drilling-induced fractures and maximum horizontal stress is at 61.2 and 318.2 degrees and the direction of the minimum horizontal stress and breakouts is at 134.five and 44.iv degrees
The minimum horizontal stress (Shmin) tin exist determined direct from the minifrac test, hydraulic fracture, or LOT/XLOT examination; nevertheless, the maximum horizontal stress (Shmax) cannot exist computed directly. Even though both of them can exist calculated using indirect methods with acceptable accuracy. The poroelastic stress equation is used in conventional means to estimate the minimum horizontal stress slope every bit a function of vertical depth. The theory of poroelasticity, which explains how a lithified, porous medium-like rock deforms when the pore space is filled with fluid and pressurized, describes the fluctuation of Sh every bit a role of. Pp (Kumpel 1991). I of the most oftentimes used approaches in the industry for determining horizontal stresses under isotropic weather is the poroelastic method. Changes in elastic stiffness characteristics acquired by structural anisotropy are used to predict the minimum and maximum horizontal stresses in this method (Abdelghany et al. 2021; Maleki et al. 2014). Equally a effect, one of the conventional methods for indirectly determining the minimum and maximum horizontal stresses is to employ the poroelastic method (Blanton and Olson 1997) (Eqs. ane, 2):
$$ Sh_{{MIN}} ~ = \frac{\upsilon }{{i~{-}\upsilon }}SV - \frac{\upsilon }{{1~ - \upsilon }}\alpha P_{P} + \alpha P_{P} + 10^{3} \frac{E}{{1 - ~\upsilon ^{2} }}\varepsilon _{10} + 10^{3} \frac{{\upsilon Due east}}{{1 - ~\upsilon ^{two} }}\varepsilon _{y} $$
(one)
$$ Sh_{{MAX}} ~ = \frac{\upsilon }{{1~{-}\upsilon }}SV - \frac{\upsilon }{{ane~ - \upsilon }}\alpha P_{P} + \alpha P_{P} + x^{three} \frac{{\upsilon E}}{{ane - ~\upsilon ^{2} }}\varepsilon _{x} + x^{three} \frac{Due east}{{1 - ~\upsilon ^{2} }}\varepsilon _{y} $$
(ii)
where \(\upupsilon \) is the Poisson'south ratio, α is Biot coefficient, P P is the pore pressure, Eastward is the static Young'southward modulus, and \(\varepsilon \) is the tectonic strain in the x and y directions (Aghajanpour et al. 2017).
Model prediction and calibration with wellbore data (observed breakouts on FMI or caliper logs) were used to place these tectonic strains. Biot coefficient or constructive stress coefficient (α) tin can be calculated using diverse parameters such as bulk modulus (Biot 1941), porosity (Krief et al. 1990), and permeability (Klimentos 2003). Theoretically, it is in the range of 0–1 (0 ≤α ≤ 1). This parameter is unremarkably derived from Eq. iii:
$$ \alpha = ~1 - \frac{{K_{b} }}{{K_{g} }} $$
(three)
where K b is the volumetric parameter of the rock total book and K thousand is the volumetric parameter of the stone grains. The British indian ocean territory coefficient was considered 1 in this analysis. If LOT/XLOT is available, the horizontal stresses are adjusted to decide the actual tectonic strain values (Gholami et al. 2015; Zoback 2010).
Fracture analysis using germination micro-imager (FMI)
Analysis of natural fractures such as determining the management of extension and slope, morphology (open or closed), density, and opening charge per unit of fractures, peculiarly in Iranian carbonate reservoirs, can be the basis of further studies. Fractures are of swell importance in the exploration, evolution of hydrocarbon fields, and hydraulic failure.
The raw data of the FMI logs are processed, analyzed, and interpreted to identify the types of fractures and also to determine the current stress direction in Santoniane carbonates (Ilam Formation) in southwestern Iran. The tectonic tendency of the fractures was determined in the wells, and the results are presented as a rose diagram of slope and the extension of discontinuities:
Figure 3 shows the results obtained from the FMI log, the extension and slope of induced fractures due to drilling operation, and maximum horizontal stress at an angle of 61.2 and 318.2 degrees (right figure). The extension and gradient of the breakouts and minimum horizontal stress are in the management of 134.v and 44.4 degrees (left figure).
Vertical stress
The pressure level exerted by combining the vertical column pressure level of various rock layers and the fluids inside themselves at a certain depth is overburden stress, commonly called vertical stress (Almalikee and Al-Najim 2018). Overburden pressure level at each point in the subsurface is due to the weight of upper layers and the office of different factors, such every bit rock blazon, porosity type, stone density, and the density of fluid filling the pores, diagenetic impact, tectonic factors, etc. This pressure includes lithostatic and hydrostatic pressures. Lithostatic pressure is the weight of the rock column, and hydrostatic pressure is the weight of the fluid column filling the pore spaces. These pressures are a function of the specific gravity of the rocks and fluids within the pores and increase in proportion to the depth. The sum of these ii pressures refers to overburden stress. In a homogeneous property, vertical stress can be easily adamant from Eq. 4:
$$ S_{V} = {\text{ }}x^{{ - 3}} _{{~\rho gz}} $$
(four)
Just in most situations, to measure the vertical stress, the initial intervals of the drilled well practise not have the density information. Consequently, a density can be calculated using a linear equation at the initial intervals from the footing to the target depth (Rana and Chandrashekhar 2015):
$$ \rho EX = \rho _{{ML}} + a_{0} (tvd - ag)^{a} $$
(v)
where ρ EX is the estimated density, ag is the distance drilling floor to ground level, tvd is the true vertical depth, ρ ML is the surface density which is almost 2 (thousand/cm3), and a and a 0 are the scale parameters in this equation (Eq. 5). The hydrostatic pressure is also determined using Eq. vi, which is the pressure level at the depth of the fluid column (Bjørlykke et al. 2015):
$$ ~P_{{h~}} = \mathop \int \limits_{0}^{z} g \times \_f~ \times ~dz $$
(6)
where ρ f is the fluid density (gm/cm3). As a consequence, with increasing depth, the pressure slope increases. For the analyzed interval, the amount of overburden stress was measured and the vertical stress gradients at the tiptop and bottom of the formations are presented in Table ane.
Ane of the vertical stress parameter applications is to utilise information technology to estimate the pore force per unit area. In that location are ii ways to measure pore pressure. The beginning technique is direct pore force per unit area measurement using special logging tools such as MDT and RFT. Pore fluid trapped in the formation porosities greatly affects the in situ stress magnitudes. Abnormal formation force per unit area yields increased complication in drilling and nonproductive times. Direct downhole measurements provide the best PP estimates; even so, these data are usually recorded only in the reservoir intervals (Sen et al., 2019, 2020; Agbasi et al. 2021; Radwan 2021b).
The second approach utilizes the indirect measurement of pore pressure from well log information such as density, resistivity, and acoustic. But experimental equations that use well logs can be used in non-reservoir periods, such as Eaton's equation (Eaton 1975). Modular Formation Dynamic Tester (MDT) tools data has been fabricated available in this analysis at reservoir intervals. The pore pressure slope was obtained from MDT pore pressure points in this reservoir.
Sonic log (DT) is sensitive to force per unit area changes because there is a relationship between porosity, compression, pore force per unit area, and sonic parameters. An increase in the depth interval of the wellbore increases compaction and in turn decreases porosity. Therefore, the bulk modulus and shear modulus increase and the compressibility decreases. By variation of these parameters, the contact surface of the grains will increment, and every bit a result, the velocity of the sonic wave volition increment. But in the high-pressure zone, the compaction rate volition decrease (Fig. 4).

Calculated pore force per unit area and its comparison with MDT results from well-testing pressure. (Track #two from left). The red dots obtained from the MDT tool that measures the pressure show a good agreement with the results of the pore pressure log
Many of the failure criteria have been proposed: Mohr–Coulomb (Coulomb 1973), Mogi–Coulomb (Mogi1971), Hoek–Brown (Chocolate-brown and Hoek 1980), and unmarried-parameter parabolic failure criteria (Li et al. 2005). It should be noted that the most common cases in the normal breakout and breakdown stress regime are Sθ >Southwardz >Sr and Sr >Sz >Sθ (Al-Ajmi 2012; Gholami et al. 2014). Several researchers take identified some issues related to the estimated values of rock forcefulness or lack of adequate cognition of stress levels in the estimated stress values for failure criteria (Vocal and Haimson 1997; Vernik and Zoback 1992). The Mohr–Coulomb failure criterion is 1 of the failure criteria that is commonly used in the oil industry due to better efficiency in terms of time and its linear consistency (Gholami et al. 2017, 2014, 2015). Of form, past ignoring the impact of intermediate stress and using the minimum and maximum stress values, this failure benchmark is used only to measure out the maximum mud pressure level for wellbore stability. This criterion'southward mathematical relationship focused on the principal stresses is as follows (Mohr 1900) (Eqs. 7, 8):
$$ S_{ane} - P_{P} = {\text{ }}UCS{\text{ }} + q\left( {S_{3} - P_{P} } \right) $$
(7)
$$ q = \frac{{\left( {1~ + ~\sin \varphi ~} \right)}}{{\left( {1 - ~\sin ~\varphi } \correct)}} $$
(viii)
The Mohr–Coulomb failure criterion's linearity is presented every bit follows (Tan et al. 2019):
$$ S_{one} = S_{C} + {\text{ }}\tan ^{2} (\frac{\pi }{four} + \frac{\varphi }{2})S_{three} $$
(nine)
where S ane and Due south three are the primary maximum and minimum stresses and South C is the unconfined compressive strength (Eq. 9). Equation 10 describes the relationship between normal and shear stress when two adhesion coefficients and internal friction angle factors are used in this benchmark:
$$ ~\tau = ~Sn~ \times ~\tan \left( \varphi \right)~ + ~C $$
(10)
where τ is the shear stress, \(\mathrm{\varphi }\) is the internal friction angle, S n is the normal stress, and C is the adhesion coefficient. Table 2 presents the calculation of mechanical failure stresses (breakout and breakdown) using the Mohr–Coulomb failure criterion in various modes of induced stresses.
Two internal friction angles and adhesion coefficient are significant parameters defined past the Mohr–Coulomb failure benchmark. It is used to determine these 2 parameters in the laboratory through iii-axis testing on drilling core samples. But there are too empirical relationships in which it is possible to quantify these parameters. The following equations are provided to quantify these two parameters:
$$ ~\varphi = {\text{ }}26.5{\text{ }} - {\text{ }}37.4\left( {one{\text{ }} - {\text{ }}NPHI{\text{ }} - V_{{shale}} } \right){\text{ }} + {\text{ }}62.one\left( {1{\text{ }} - {\text{ }}NPHI{\text{ }} - V_{{shale}} } \right)^{ii} $$
(11)
$$ C = UCS \times {\text{ }}(one - \sin \varphi /~2{\text{ }}\cos \varphi )~ $$
(12)
where \(\mathrm{\varphi }\) is the internal friction angle, NPHI is the neutron porosity, V shale is the shale volume (commonly calculated from the gamma-ray log), UCS is the uniaxial stress, and C represents the adhesion coefficient (Eqs. eleven,12).
In the shale segment, the internal friction angle and Young'due south coefficient are decreasing; on the contrary, these related subjects increase in thick limestone segments such as Ilam and Mishrif. Too, the Poisson'due south ratio in all formations decreases relatively with an increase in shale book (Table3).
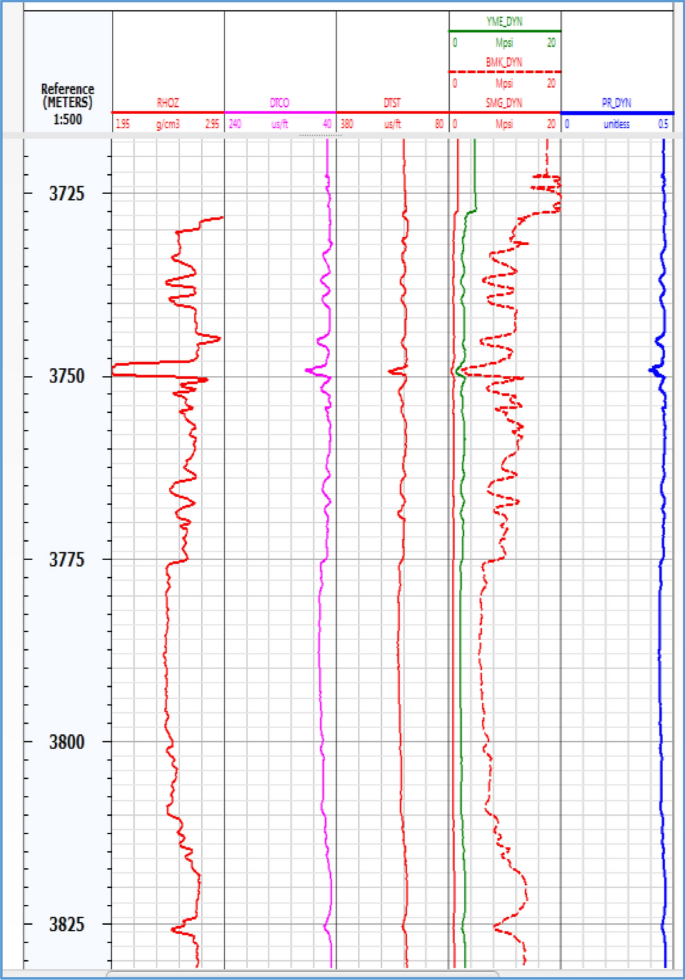
Effigy v shows the results of dynamic parameters, which include the following from left to right, respectively:
Poisson's ratio, Young'south modulus, and UCS dynamic parameter results
The first track includes logs of drill bit size (BS), well bore (CAL), and amount of radioactivity (SGR) which are considered in understanding with dynamic parameters. The second rail represents Young'southward modulus, which is lower in the shaly interval than in the limestone interval. The 3rd and 4th tracks show the Poisson'south ratio and rigidity, which increases as a bulk modulus in track five in limestone and decreases in shaly formations. The sixth and seventh tracks, which include the compressional shear moving ridge velocity and the Poisson ratio, respectively, show a good agreement with lithology too equally other dynamic parameters.
The obtained results of UCS, the Poisson'southward ratios, the Immature coefficient, and the prophylactic drilling deviation bending are shown in Tabular array 4. These results in the reservoir segment all comprise Ilam and Mauddud formations with more than 150 MPa unconfined compressive strength (UCS). The Poisson's ratio is less than 0.25 psi, and the Young's coefficient is between 80 and 64 GPa. Considering the calculated results, the optimum wellbore difference angle for the reservoir segment is more than 45° (277° azimuth). These calculations for shale and flysch Gurpi segments are variable, so the amount of UCS has a range of changes from 30 to 150 MPa, Poisson's ratio from 0.25 psi to 0.iii psi, and Young's coefficient included some changes from 32 to 64GPa.
The calculated issues in different Gurpi formation segments and safe drilling trajectories indicated 30° to 45° deviation.
In Table 5, formations depth and their intervals are provided with lithology blazon.
The effect of wellbore's azimuth and diversion on mud weight window and rubber mud weight window estimation
To calculate the geomechanical parameters, raw information and information of drilling wells in the Ilam, Mauddud, Mishrif and Khatiyah formations are collected. Petrophysical and geomechanical evaluation of the mentioned formations is investigated and performed (Fig. half-dozen). Figure 6 illustrates the acoustic, density, shear, Immature's modulus, and Poisson's ratio logs.
Density, sonic, shear, Young'south modulus, and Poisson'south ratio
In Fig. six, the first track from the left represents the density log, which shows the lithological changes with respect to depth. In the second and third tracks, the sonic logs testify the changes in sonic slowness at different depths, which increase with decreasing density and vice versa. The fourth rail is Immature's modulus, which increases in magnitude and velocity with increasing density which shows a smaller value in clay content, and its low value indicates a decrease in the amount of bulk and shear modulus. The fifth track shows the Poisson'due south ratio increasing in carbonate formations compared to shaly formations, which bespeak more stability in the carbonate formations.
To calculate the dynamic and static geomechanical parameters, information technology is necessary to calculate the uniaxial compressive strength (UCS) and the equivalent mud weight (EMW) which is the mud weight needed to remainder formation fluid pressure level. In Figs. 7 and viii, Young'southward modulus and Poisson'southward ratio window are used to summate the UCS and EMW. In this section, shale volume log is also used to validate these calculations.
In Figs. vii and 8, the first track from the left, a gamma-ray log is displayed, which shows the shale volume. In the 2d rail, the UCS log shows that the uniaxial compressive strength has drastic changes in the studied formations and that the highest compressive strength is observed in limestone and calcite thick layers. In this rails, both static and dynamic values are depicted side by side, which validates the results obtained from the dynamic log. In the third and fourth tracks, Immature's modulus and the equivalent mud weight (EMW) logs are shown. These logs indicate that the drilling mud weight increases in areas of shale where Young's modulus decreases. Also, the calculated drilling mud weight indicates that in the intervals where the amount of uniaxial compressive strength decreases, the corporeality of mud weight increases to increase wellbore stability (Fig. vii).
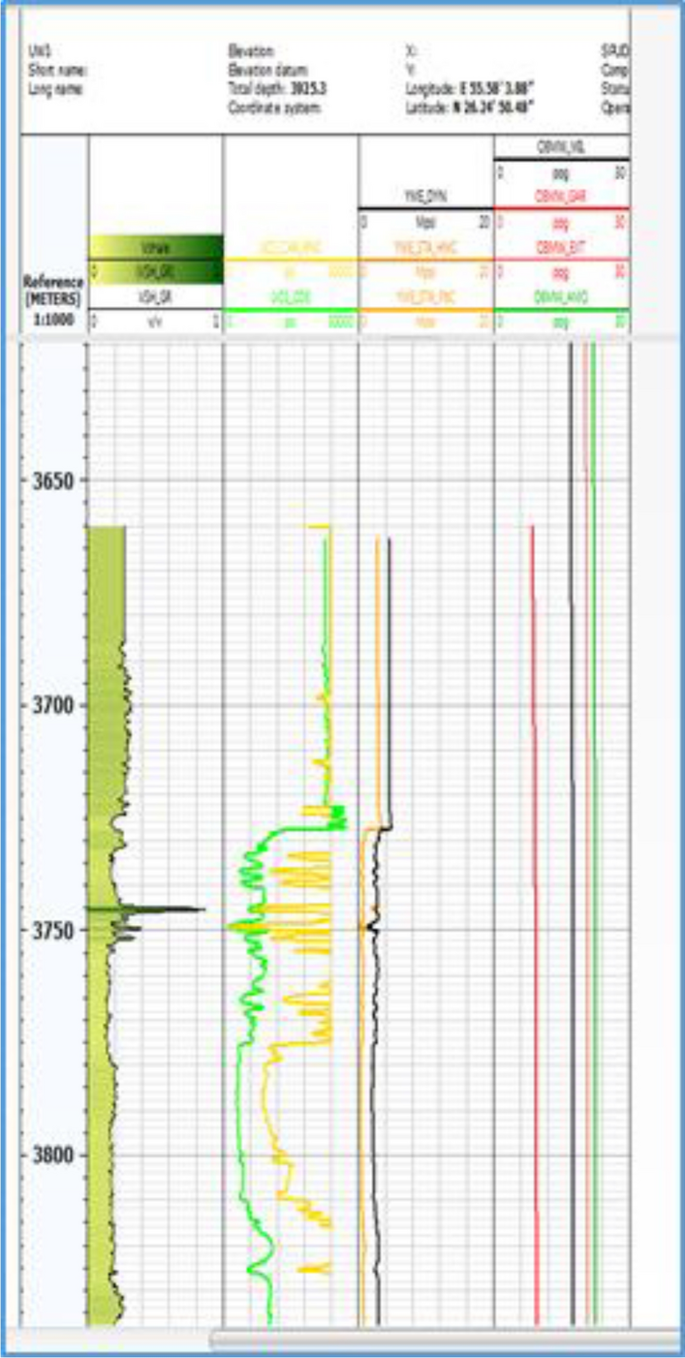
Static and dynamic computation of the EMW, UCS, and Immature's modulus
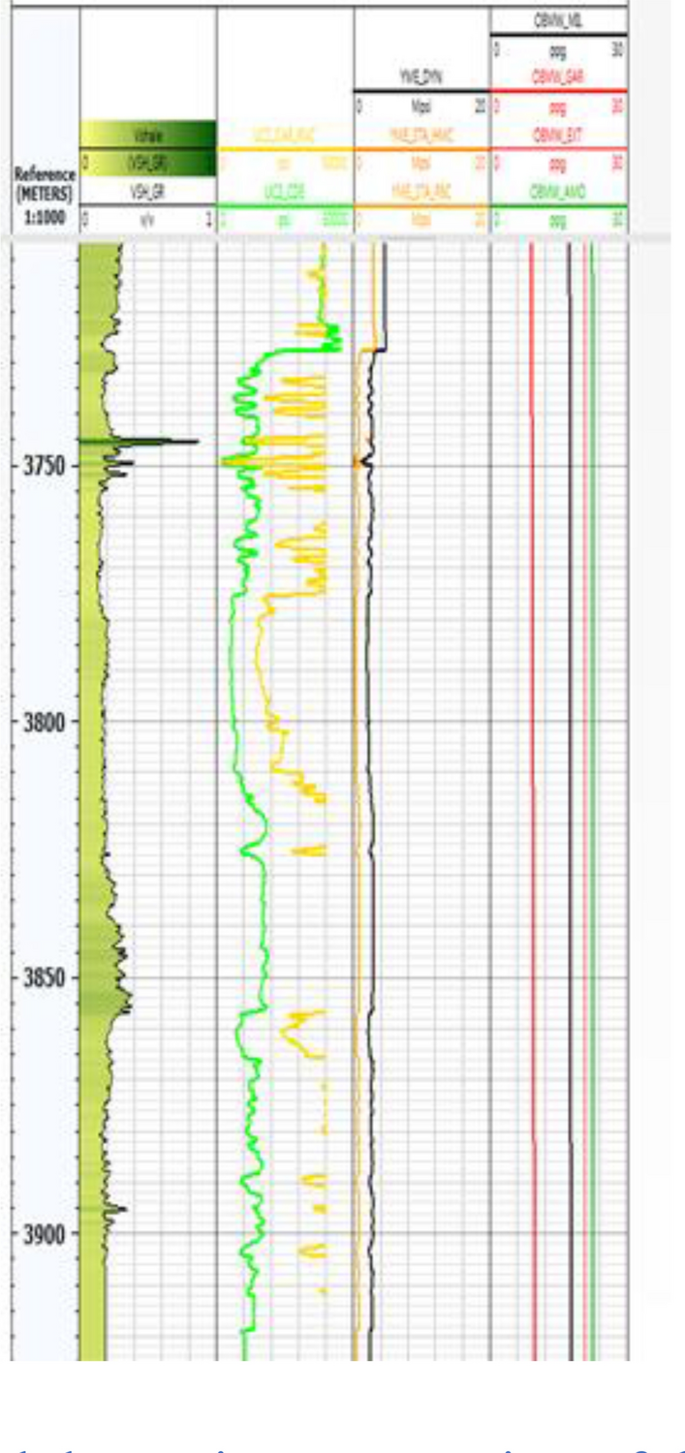
Static and dynamic ciphering of the EMW, UCS, and Immature's modulus
Estimation of mud weight window
Optimum mud weight estimation comprises an allowable range of drilling mud weight. Mechanical earth modeling (MEM) analyzes wellbore stability based on failure criteria. Failure criterion is a mathematical equation that models the behavior of a rock at the moment of failure. Coulomb (1776) introduced the simplest yet most of import failure criterion. Co-ordinate to this criterion, rock failure will occur when shear stress in a plane overcomes the strength of friction and rock cohesion in that plane. According to Mohr'south theory, friction in a airplane is opposite to the direction of motion, and its value is straight proportional to the tension that compresses the two planes. Therefore, this criterion can be written as follows (Colmenares and Zoback 2002):
$$ \tau = C + \mu \sigma _{north} $$
(13)
\({\sigma }_{north}\) influences perpendicular to the fracture aeroplane and plays a positive role in stone stability. In the above equation, \(\tau \) is the coefficient of internal friction and C is the cohesion (Eq. 13). The master disadvantage of the MC criterion is to ignore the effect of intermediate stress. In this failure criterion, the intermediate stress does not affect the normal and shear stresses. Moreover, information technology is assumed that intermediate stress does not affect the occurrence of stone failure. MC failure benchmark can be expressed past maximum (\(\sigma \) 1) and minimum (\(\sigma \) 3) principal stresses. The maximum and minimum principal stresses can be easily calculated from Mohr'south circumvolve (Gholami et al. 2014):
$$ \sigma _{n} = \frac{{(\sigma _{1} + \sigma _{3} ) + (\sigma _{1} - \sigma _{3} )\cos \left( {2\theta } \right)~}}{two} $$
(14)
$$ \tau = \frac{{\sigma _{1} - \sigma _{3} ~}}{ii}\sin \left( {2\theta } \right) $$
(15)
In the above equations, \(\uptheta \) is the angle between normal to the plane and maximum chief stress direction (Eq. 14, xv).
$$ ~\theta ~ = \frac{\pi }{4} + \frac{\varphi }{2} $$
(sixteen)
In the higher up equation, \(\varphi \) (angle of internal friction) is the refraction angle that tin theoretically alter from 0 \(^\circ \) to ninety \(^\circ \). However, the practical range of changes in this angle is smaller and ranges from 0 \(^\circ \) to 30 \(^\circ \), so, co-ordinate to the above equation, it is obvious that Ten can vary betwixt 45 \(^\circ \) and 90 \(^\circ \) (Eq. sixteen).
Figure 9 specifies the low level of drilling mud weight in blackness colour. If the weight of drilling fluid reaches lower than the black line, borehole collapse pressure would occur and might bring up wellbore plummet in shale formations and brand the bore bigger or smaller. In the lower level of the least mud weight, the shear failure tin occur, called collapse pressure.
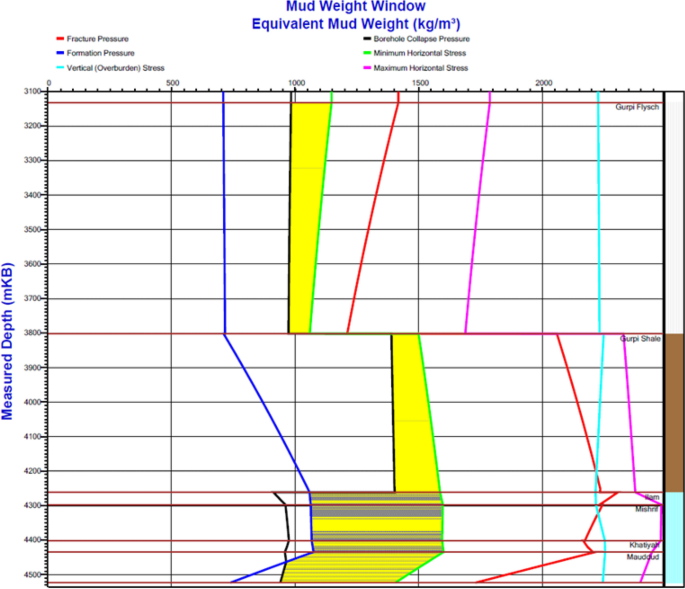
Mud window in the wellbore trajectory desired past Mohr–Coulomb failure criterion under mechanical conditions, fracture slope, and formation pressure in the Gurpi, and Mauddud formations in the study expanse (the drilling safe mud weight windows are shown with yellow colour)
Tensile failure occurs in the upper meters near the surface, while shear failure takes place at greater depth, beneath which, failure does not occur. The tensile failure region shown in carmine color is related to the failure pressure of the formation or high drilling mud weight level. It implies that if the weight of drilling fluid inside the wellbore is more than the ruby-red line, it might bring up a tensile failure. It increases the probability of archway of drilling fluid to the formations, namely lost circulation.
A higher amount leads to the tensile failure range called fracture pressure level (Gao et al. 2019a, b, c). Shearing strength is often defined past the Mohr–Coulomb failure criterion and ii parameters: failure envelope cohesion and internal friction angle.
Regarding the results, whatever observed in Gurpi germination shows a distinct value in the weight of drilling fluid and other geophysical parameters such every bit maximum horizontal stress, formation pore pressure (Gao et al., 2019a; Radwan 2021; Baouche et al. 2021), the safe mud window range between minimum horizontal stress and minimum mud weight for wellbore collapse, shear failure, and tensile failure. Consequently, these changes indicate the shale segment in the depth of 3800 1000. Therefore, to preserve wellbore stability, it is vital to increment the weight of drilling fluid. In the Ilam and Khatiyah formations, the weight of the drilling fluid window is increased, whereas some changes occurred in other parameters, which are presented beneath: Albeit the weight of drilling fluid in the reservoir area in the Ilam is decreased, the maximum horizontal stress is increased. In this surface area, the formation pressure indicates changes in the shear failure region from the least level of mud weight to the least level of formation fluid pressure.
In Khatiyah formation, the maximum horizontal stress is decreased. By dissimilarity, the loftier level of mud weight increases, reducing the tensile failure boundary (Fig. 9).
Figures 10, 11, and 12 depict safe zones in terms of mud weight and drilling management, indicating certain stable and unstable depths along the investigated well. The bluish colour in Stereonets denotes the safe locations for drilling orientation without whatsoever breakout or breakup (stable orientation), whereas the red color denotes the unstable orientation. The mud weight employed at that depth is shown past the bespeak marked on these figs. The optimal difference, azimuth, and mud weight are provided to forbid shear and tensile failures. Figures 10, eleven, and 12 are the typical polar plots in STABview. The geomechanical analysis indicates that the direction of minimum horizontal stress (σh) and maximum horizontal stress) σH (in Gurpi is NW–SE and NE–SW. Drilling more than 50° deviations in Gurpi formation might bring up diverse problems such as wellbore breakup. Therefore, the safe mud weight window in Gurpi formation is from xi.18 to 12.61 ppg, with 35° drilling inclination and 277° azimuth (Fig. ten). It should exist noted that 1 pound per gallon (ppg) is equivalent to seven.48 pounds per cubic foot (pcf).
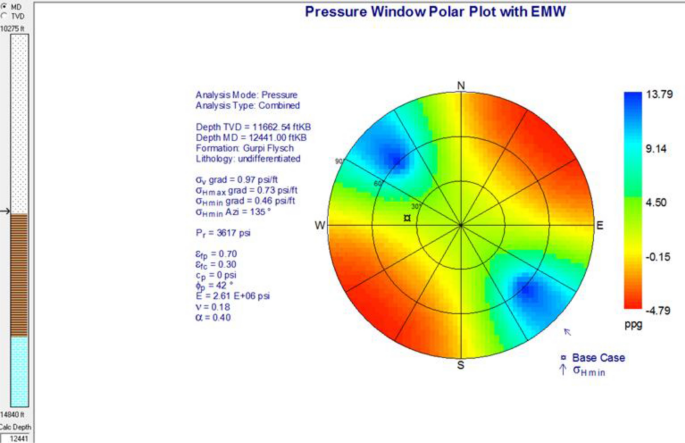
Direction of the minimum horizontal stress and the maximum horizontal stress
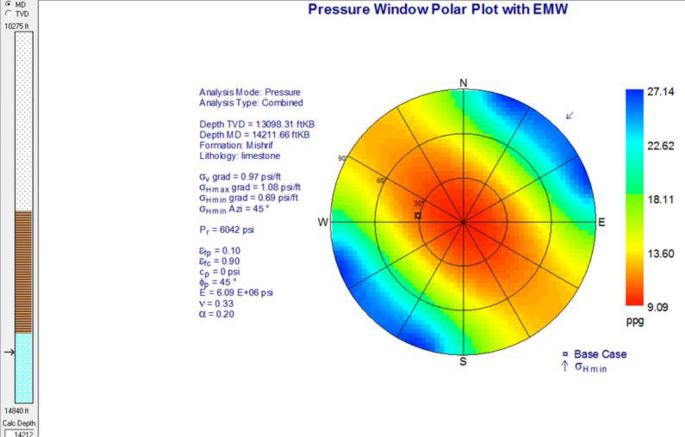
Azimuth effect and wellbore inclination on mud weight windows in the Mishrif interval

Azimuth and wellbore inclination on mud weight windows in the Ilam interval
The direction of minimum horizontal stress (σh) and maximum horizontal stress (σH) in the Mishrif and Ilam formations is NE–SW and NW–SE, respectively. Drilling more than 60° inclination in the Mishrif and Ilam formations might bring up different problems such equally wellbore breakout. Therefore, the equivalent mud weight window for the Ilam and Mishrif formations is nine.36 to 13.13 ppg, with 45° drilling inclination and 277° azimuth.
Word
The geomechanical modeling approach presented here is used to provide a more than appropriate representation of a stable mud weight window past applying a geomechanical analysis incorporated with UCS, the Poisson's ratios, and Young'due south modulus. Haider Qasim et al. 2017 worked on wellbore instability problems. They conducted that a diversity of factors play a significant role in controlling the instability hassles and in determining an optimum mud weight to avert sticking and borehole plummet pressure, which might bring upwardly wellbore plummet in shale formations and make the bore bigger or smaller.
Haider Qasim et al. (2017) determined the in situ stress and induced stresses using numerous field and laboratory information from the study area. It is carried out by analyzing wellbore failure, core analyses, and field tests such as the triaxial exam and minifrac which are vital to improving geomechanical modeling (Abdelghany et al. 2021). In dissimilarity, in this written report, no core samples nor the core data were available to be used; therefore, using a compressional moving ridge velocity log, reservoir geomechanical parameters are calculated. The sonic log measures shear wave and compressional moving ridge velocities with medium density.
Moreover, with a proper format in Techlog, we yielded dynamic parameter estimations such as the Poisson's ratio, Young'southward modulus, bulk modulus, and other geomechanical parameters of the numerical information process.
Bagheriet al. (2021) used conventional well logs, DSI log, FMI log, petrophysical evaluation results (mineral and porosity), and pore force per unit area points from MDT tools. In this work, we accept compared our data with Bagheri et al. (2021) to figure out how our findings in 1 of the Iranian hydrocarbon reservoirs are far or similar. From our point of review, in Sarvak formation, we have simply divided geomechanical properties based on three different formations (Ilam, Sarvak, Gurpi), and to get the values for each germination, nosotros extracted them to half dozen categories (Gurpi Flysch, Gurpi shale, Ilam, Mishrif, Khatiyah, Mauddud) so divided the issue by six to ascertain the boundaries of the proposed six formations. As far as the reservoir section consists of Ilam and Sarvak formations, we subtracted them to one section to calculate UCS and Phi. The Middle Sarvak Formation (Cenomanian) is believed to exist an important source rock within the Cretaceous petroleum system of the eastern Persian Gulf basin (Alipour 2017; Hosseiny et al. 2016), and every bit far as Baghery et al. (2021) worked on the same reservoir system (Middle Cretaceous (Albian–Thoronian)), we carried out our findings that are similar to them, whereas, by using a simple arroyo, we separated different formations to make information technology more sensible. Equivalent mud weight values in Gurpi formation range from eleven.xviii to 12.61 ppg and in Ilam and Mishrif formations (reservoir section) fluctuated from 9.36 to 13.13 ppg. Similarly, Baghery et al. (2021) concluded that the equivalent mud weight for the reservoir section is from ten to sixteen.8 ppg.
Sensitivity analysis determines how different values of an independent variable affect a particular dependent variable nether a given set of assumptions. In other words, sensitivity analyses study how diverse sources of uncertainty in a mathematical model contribute to the model's overall uncertainty. Tornado charts are usually used for sensitivity analysis, past facilitating the comparison of the effects of one variable (or uncertainty) on the output (value) of an contained variable. Sensitivity assay is performed using tornado plot. Sensitivity analysis reveals the sensitivity of the model to the input parameter variations. The tornado plot is pivotal to agreement some parameters that demand to be more accurately counted every bit practical and useful parameters placed in the plot. Some parameters with maximum variations are placed at the top of the nautical chart. On the contrary, the parameters with minimum variations are placed lower (Fig. 13). The most useful parameter on equivalent mud weight is the maximum horizontal stress slope. On the other hand, the Young'south modulus and Poisson's ratio are the to the lowest degree important (Fig. 13).
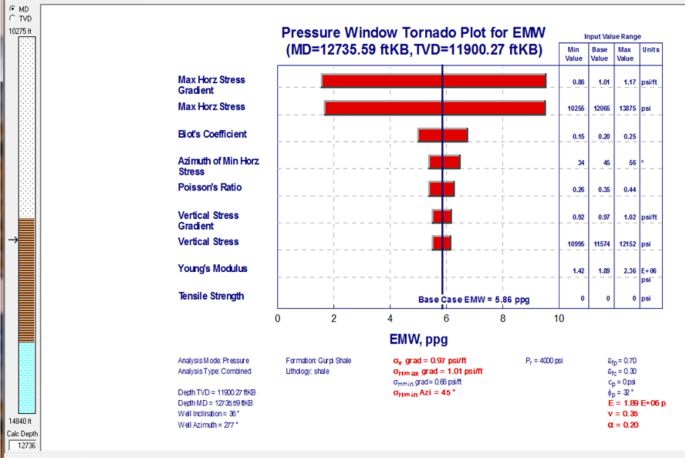
Yielded results of sensitivity assay tornado
Concluding remarks
It was found that the wellbore trajectory and drilling fluid density in operation have a significant impact on the wellbore stability in the study area. Core measurements are very of import to evangelize reliable results, whereas, in our report, no core samples nor the cadre data were available to be used. Still, we have used other datasets utilizing well log data, drilling, and geological data to create a wellbore stability model applicable in the written report area. The unconfined compressive strength (UCS) value in the reservoir zone, including Ilam to Mauddud formations, shows that the condom inclination angle is more than 45° (277° azimuth); alternatively, drilling more than sixty° might bring up different problems such as collapse, boot, increasing drilling costs, and stopping production and somewhen might indeed cause well loss. Consequently, the condom inclination angle for Gurpi germination is 35°, and drilling more l° might bring up diverse problems such as wellbore breakout, wash-out, or tightening.
Geomechanical analysis based on geomechanical parameters illustrates that the direction of minimum horizontal stress and maximum horizontal stress in Gurpi formation is NW–SE and NE–SW, and for Mishrif and Ilam formations is NE-SW and NW–SE, respectively.
Sensitivity analysis shows that the most meaning parameter in the mud weight window is maximum horizontal stress; by contrast, Poisson's ratios and Young's modulus are the least important.
Abbreviations
- E :
-
Young's modulus, GPa (Mpsi)
- G :
-
Shear modulus, GPa (Mpsi)
- K :
-
Bulk modulus, GPa (Mpsi)
- S Hmax :
-
Maximum horizontal stress, MPa (psi)
- S hmin :
-
Minimum horizontal stress, MPa (psi)
- 5 p :
-
Compressional wave velocity, k/sec (ft/sec)
- μ :
-
Shear modulus
- λ :
-
Lame'due south coefficient
- V s :
-
Shear wave velocity, grand/sec (ft/sec)
- ΔP :
-
Deviation between wellbore pressure and pore force per unit area, MPa (psi)
- ρ :
-
Bulk density, g/cmthree (kg/m3)
- ρ w :
-
Water density, thou/cmiii (kg/chiliad3)
- σ :
-
Stress, MPa (psi)
- σ ane :
-
Maximum principle stress, MPa (psi)
- σ 2 :
-
Intermediate principle stress, MPa (psi)
- σ 3 :
-
Minimum principle stress, MPa (psi)
- σ r :
-
Radial stress at the wellbore, MPa (psi)
- σ y :
-
Stress in y-axis in Cartesian coordinate system, MPa (psi)
- σ z :
-
Axial stress at the wellbore, MPa (psi)
- σ zz :
-
Stress in z-centrality in Cartesian coordinate system, MPa (psi)
- \({\varepsilon }_{\mathrm{zz}}\) ε zz :
-
Axial tensile strain ε xx
- \({\varepsilon }_{\mathrm{\blastoff \alpha }}\) :
-
Bulk strain
- \({\sigma }_{0}\) :
-
Or ΔP is the hydrostatic stress
- \(v\) :
-
Poisson's ratio, dimensionless;
- \({\sigma }_{\mathrm{c}}\) :
-
Uniaxial rock strength
- \({\sigma }_{\mathrm{t}}\) :
-
Tangential stress, MPa;
- \({\sigma }_{\mathrm{h}}\) :
-
Minimum horizontal stress, MPa;
- \(\alpha \) :
-
Biot coefficient;
- \(V\) :
-
Poisson'south coefficient
- \({\sigma }_{\mathrm{V}}\) :
-
Total (volumetric) mean stress
- \({P}_{\mathrm{f}}\) :
-
Drilling fluid pressure level
- Due east :
-
Elasticity modulus (Gpa)
- \({\varepsilon }_{\mathrm{H}}\) :
-
Tectonic strains in maximum horizontal stresses
- \({\varepsilon }_{\mathrm{h}}\) :
-
Tectonic strains in minimum horizontal stresses
- \({\sigma }_{\mathrm{H}}\) :
-
Maximum horizontal stress, MPa;
- E :
-
Elasticity modulus
- ε ax :
-
Strain in axial direction x
- σ x :
-
Centric strain in axial direction x
- υ :
-
Poisson'southward coefficient
- σ θ ' :
-
Hoop stress alteration due to the introduction of osmotic pressure level, MPa (psi)
- τ :
-
Shear stress, MPa (psi)
- υ :
-
Poisson's ratio, unitless
- Ф :
-
Internal friction angle, degrees
- φ :
-
Wellbore azimuth, degrees
- Ø :
-
Germination porosity, fraction
- DTC and DTs:
-
Compressional slowness and shear slowness (sonic log)
- FMI:
-
Germination micro-imager
- DSI:
-
Dipole shear sonic imager
- MDT:
-
Modular formation dynamics tester
- ρ and ρb and RHOB:
-
Density
- D and Z and dz:
-
Depth
- g :
-
Gravity
- tvd:
-
True vertical depth
- Ph:
-
Hydrostatic pressure level
- PP:
-
Pore pressure
- Edyn and Esta:
-
Young'southward dynamic modulus and Immature's static modulus
- ν dyn and ν sta :
-
Dynamic Poisson'due south ratio and static Poisson's ratio
- UCS:
-
Uniaxial compressive strength
- α and British indian ocean territory:
-
Biot coefficient
- Cane and C2:
-
Caliper 1 and caliper 2
- LOT/XLOT:
-
Lake off test and extended leak off test
- ε :
-
Tectonic strain
- FIT:
-
Formation integrity exam
- Southwardθ and Sz and Sr:
-
Tangential stress and centric stress and radial stress
- C :
-
Adhesion coefficient
- φ :
-
Internal friction bending
- NPHI:
-
Neutron porosity
- Fiveshale:
-
Shale volume
- CMW_KICK:
-
Kicking pressure
- CMW_LOSS:
-
Mud loss
- CMW_MAX_MTS:
-
Breakdown pressure
- CMW_MIN_MC:
-
Shear failure minimum pressure
- MW:
-
Mud weight
- KICK-BREAKOUT:
-
Difference between shear failure and kicking
- LOSS-BREAKDOWN:
-
Difference between loss and tensile failure
- AIc:
-
Compressional acoustic impedance
- AIs:
-
Shear impedance
- RCc:
-
Compressional reflection coefficient
- RCs:
-
Shear reflection coefficient
- Sv and Sn:
-
Vertical stress and normal stress
- PHIE:
-
Effective porosity
References
-
Abdelghany WK, Radwan AE, Elkhawaga MA, Wood D, Sen Southward, Kassem AA (2021) Geomechanical modeling using the depth-of-damage approach to achieve successful underbalanced drilling in the gulf of suez rift basin. J Petrol Sci Eng. https://doi.org/x.1016/j.petrol.2020.108311
-
Agbasi Southward, Sen N, Joseph Inyang S, Etuk E (2021) Cess of pore pressure, wellbore failure and reservoir stability in the Gabo field Niger Delta, Nigeria. Implic Drill Reserv Manag. https://doi.org/10.1016/j.jafrearsci.2020.104038
-
Aghajanpour A, Fallahzadeh SH, Khatibi S, Hossain MM, Kadkhodaie A (2017) Total waveform acoustic data every bit an aid in reducing uncertainty of mud window design in the absence of leak-off test. J Nat Gas Sci Eng 45:786–796
-
Al-Ajmi AM (2012) Mechanical stability of horizontal wellbore implementing Mogi-coulomb police. Adv Pet Explor Dev iv(two):28–36
-
Al-Ajmi AM, Zimmerman RW (2006) Stability assay of vertical boreholes using the Mogi-Coulomb failure criterion. Int J Rock Mech Mining Sci 43(8):1200–1211
-
Alipour, Alizadeh B, Chehrazi A (2017) A thermal maturity analysis of the effective cretaceous petroleum system in the southern farsi gulf basin may 2017 oil & gas science and technology, Revue de l IFP doi: https://doi.org/x.22050/IJOGST.2017.53898
-
Alizadeh M, Alipour A, Chehrazi (2017) Chemometric classification and geochemistry of oils in the Iranian sector of the southern Persian Gulf Basin. Org Geochem. https://doi.org/x.1016/j.orggeochem.2017.05.006
-
Almalikee HSA, Al-Najim FMS (2018) Overburden stress and pore pressure prediction for the Northward Rumaila oilfield. Republic of iraq Model Earth Syst Environ iv(3):1181–1188
-
Bagheri H, Tanha AA, Doulati Ardejani F, Heydari-Tajareh K, Larki Eastward (2021) Geomechanical model and wellbore stability analysis utilizing acoustic impedance and reflection coefficient in a carbonate reservoir. J Petrol Explor Prod Technol 11:3935–3961. https://doi.org/10.1007/s13202-021-01291-2
-
Baouche R, Sen S, Chaouchi R, Ganguli SS (2021) Modeling in-situ tectonic stress state and maximum horizontal stress azimuth in the Cardinal Algerian Sahara - a geomechanical study from EL Agreb, EL Gassi and Hassi Messaoud fields. J Nat Gas Sci Eng 88:103831. https://doi.org/10.1016/j.jngse.2021.103831
-
British indian ocean territory MA (1941) General theory of three-dimensional consolidation. J Appl Phys 12(2):155–164
-
Bjørlykke K, Høeg 1000, Mondol NH (2015) Introduction to Geomechanics: stress and strain in sedimentary basins. Petroleum geoscience. Springer, Berlin, pp 301–318
-
Blanton T, Olson JE (1997) Stress magnitudes from logs: effects of tectonic strains and temperature. In: SPE almanac technical conference and exhibition. Lodge of petroleum engineers
-
Brown E, Hoek E (1980) Underground excavations in rock. CRC Printing, London
-
Colmenares and Zoback (2002) A statistical evaluation of intact rock failure criteria constrained by polyaxial exam information for five different rocks. Int J Rock Mech Mining Sci. https://doi.org/x.1016/S1365-1609(02)00048-5
-
Coulomb CA (1973) Essai sur une awarding des regles de maximis et minimis a quelques problemes de statique relatifs a l'compages (essay on maximums and minimums of rules to some static issues relating to compages)
-
Darvishpour A, Seifabad MC, Woods DA, Ghorbani H (2019) wellbore stability analysis to decide the safe mud weight window for sandstone layers. Pet Explor Dev 46(five):1031–1038
-
Das B, Chatterjee R (2017) Wellbore stability analysis and prediction of minimum mud weight for few wells in Krishna-Godavari Basin, India. Int J Rock Mech Min Sci 93:30–37
-
Eaton BA (1975) The equation for geopressure prediction from well logs. In: Fall meeting of the society of petroleum engineers of AIME. Society of petroleum engineers
-
Gao Q, Cheng Y, Han Southward, Yan C, Jiang L (2019) Numerical modeling of hydraulic fracture propagation behaviors influenced past pre-existing injection and production wells. J Pet Sci Eng 172:976–987. https://doi.org/x.1016/j.petrol.2018.09.005
-
Gao Q, Han S, Cheng Y, Yan C, Sun Y, Han Z (2019) Effects of non-uniform pore pressure field on hydraulic fracture propagation behaviors. Eng Fracture Mech. https://doi.org/10.1016/j.engfracmech.2019.106682
-
Gao Q, Cheng Y, Han South, Yan C, Jiang Fifty, Han Z, Zhang J (2019) Exploration of not-planar hydraulic fracture propagation behaviors influenced by pre-existing fractured and unfractured wells. Eng Fracture Mech. https://doi.org/10.1016/j.engfracmech.2019.04.037
-
Ghazban F (2007) Petroleum geology of the Persian Gulf, Tehran University and National Iranian Oil Company press
-
Gholami R, Moradzadeh A, Rasouli 5, Hanachi J (2014) Practical application of failure criteria in determining safe mud weight windows in drilling operations. J Stone Mech Geotech Eng 6(one):13–25
-
Gholami R, Rasouli V, Aadnoy B, Mohammadi R (2015) Application of in situ stress estimation methods in wellbore stability assay under isotropic and anisotropic weather. J Geophys Eng 12(4):657–673
-
Gholami R, Aadnoy B, Foon LY, Elochukwu H (2017) A methodology for wellbore stability analysis in anisotropic formations: a instance written report from the Canning Bowl, Western Commonwealth of australia. J Nat Gas Sci Eng 37:341–360
-
Gholilou P, Behnoudfar South, Vialle Grand, Madadi, (2017) Determination of safe mud window considering time-dependent variations of temperature and pore pressure analytical and numerical approaches. J Rock Mech Geotech Eng. https://doi.org/10.1016/j.jrmge.2017.02.002
-
Heller R, Zoback M (2014) Adsorption of methane and carbon dioxide on gas shale and pure mineral samples. J Unconv Oil Gas Resour viii:14–24. https://doi.org/10.1016/j.juogr.2014.06.001
-
Hosseiny A, Rabbani Reza, Seyed A, Moallemi, (2016) Source stone characterization of the Cretaceous Sarvak Formation in the eastern part of the Iranian sector of Persian Gulf. Org Geochem. https://doi.org/ten.1016/j.orggeochem.2016.06.005
-
James GA, Wynd JG (1965) Stratigraphic classification of Iranian Oil Consortium Agreement Area Am. Assoc Petrol Geol Bull 49:2182–2245
-
Kassem AA, Sen S, Radwan AE, Abdelghany WK, Abioui Yard (2021) Effect of depletion and fluid injection in the mesozoic and paleozoic sandstone reservoirs of the october oil field central gulf of suez bowl implications on drilling production and reservoir stability. Nat Resources Res. https://doi.org/10.1007/s11053-021-09830-8
-
Klimentos T (2003) NMR applications in petroleum related rock mechanics: sand control, hydraulic fracturing, wellbore stability. In: SPWLA 44th annual logging symposium. OnePetro
-
Kumpel HJ (1991) Poroelasticity: parameters reviewed. Geophys J Int. https://doi.org/10.1111/j.1365-246X.1991.tb00813.x
-
Le K, Rasouli V (2012) Determination of condom mud weight windows for drilling deviated wellbores: a case study in the North Perth Basin. WIT Trans Eng Sci xxx(81):83–95
-
Li C-G, Zheng H, Ge X-R, Wang S-Fifty (2005) Enquiry on two-parameter parabolic Mohr strength criterion and its damage regularity Yanshilixue Yu Gongcheng Xuebao/chin. J RockMech Eng 24(24):4428–4433
-
Li S and Zhang J (2011) Wellbore stability modeling and real-fourth dimension surveillance for deepwater drilling to weak bedding planes and depleted reservoirs. SPE/IADC 139708 presented at the SPE/IADC Drilling Conference and Exhibition held in Amsterdam, The Netherlands
-
Maleki Due south et al (2014) Comparison of different failure criteria in prediction of safe mud weigh window in drilling practice. Earth Sci Rev 136:36–58
-
Mogi Chiliad (1971) Fracture and flow of rocks under high triaxial compression. J Geophys Res 76(5):1255–1269
-
Mohr O (1900) Welche umstande bedingen dice elastizitatsgrenze und den bruch eines materials. Z Ver Dtsch Ing 46(1524–1530):1572–1577
-
Nelson Eastward, Hillis R, Mildren Due south (2006) Stress partitioning and wellbore failure in the West Tuna Area. Gippsland Basin Explor Geophys 37(3):215–222
-
OEOC (2014) PC2000 Marine seismic operation. http:// world wide web. oeoc. ir/marine-operations. html. Accessed on 2014.
-
Peng Southward, Wang X, Xiao J, Wang 50, Du M (2001) Seismic detection of rockmass damage and failure zone in tunnel. J China Univ Min Tech xxx(1):23–26 ((in Chinese))
-
Radwan AE (2021) Modeling pore pressure level and fracture pressure using integrated well logging, drilling based interpretations and reservoir data in the Giant El Morgan oil Field, Gulf of Suez Egypt. J African Earth Sci. https://doi.org/10.1016/j.jafrearsci.2021.104165
-
Radwan A, Sen Southward (2020) Stress path analysis for characterization of in situ stress state and effect of reservoir depletion on present-day stress magnitudes: reservoir geomechanical modeling in the Gulf of Suez Rift Bowl. Egypt Nat Resources Res 30:463–478. https://doi.org/x.1007/s11053-020-09731-2
-
Radwan AE, Sen S (2021) Characterization of in-situ stresses and its implications for production and reservoir stability in the depleted El Morgan hydrocarbon field Gulf of Suez Rift Bowl Egypt. J Struct Geol. https://doi.org/10.1016/j.jafrearsci.2019.103743
-
Radwan A, Abudeif A, Attia Yard, Mohammed M (2019) Pore and fracture force per unit area modeling using direct and indirect methods in Badri Field, Gulf of Suez. Egypt J Afr Earth Sci 156:133–143
-
Radwan AE, Abudeif AM, Attia MM, Elkhawaga MA, Abdelghany WK, Kasem AA (2020) Geopressure evaluation using integrated basin modelling, well-logging and reservoir information analysis in the northern part of the Badri oil field, Gulf of Suez Arab republic of egypt. J African Earth Sci 162:103743. https://doi.org/10.1016/j.jafrearsci.2019.103743
-
Radwan AE, Abdelghany WK, Abdelghany WK (2021) Nowadays-mean solar day in-situ stresses in Southern Gulf of Suez, Egypt: Insights for stress rotation in an extensional rift basin. J Struct Geol. https://doi.org/10.1016/j.jsg.2021.104334
-
Rahimi M, Riahi MA (2020) Static reservoir modeling using geostatistics method: a case report of the Sarvak Formation in an offshore oilfield. Carbonates Evaporites 35:62. https://doi.org/x.1007/s13146-020-00598-i
-
Rahimi R (2014) The consequence of using dissimilar rock failure criteria in wellbore stability assay, MS Thesis, Missouri University of Science and Technology
-
Rana R, Chandrashekhar C (2015) Pore pressure prediction a example written report in Cambay basin. Geohorizons twenty(1):38–47
-
Razin FT, van Buchem, (2010) Sequence stratigraphy of Cenomanian-Turonian carbonate platform margins (Sarvak Formation) in the High Zagros, SW Iran: An outcrop reference model for the Arabian Plate pril 2010. Geol Soc London Special Pub 329(ane):187–218. https://doi.org/10.1144/SP329.9
-
Sen Southward, Kundan A, Kalpande 5, Kumar M (2019) The present-day state of tectonic stress in the offshore Kutch-Saurashtra Basin, India. Mar Pet Geol 102:751–758. https://doi.org/10.1016/j.marpetgeo.2019.01.018
-
Sen Due south, Kundan A, Kumar Thousand (2020) Modeling pore pressure, fracture pressure and collapse pressure gradients in offshore Panna, Western Bharat, implications for drilling and wellbore stability. Nat Resour Res. https://doi.org/10.1007/s11053-019-09610-5
-
Sen S, Ganguli SS (2019) Estimation of pore pressure and fracture slope in Volve Field, Norwegian North Bounding main. In SPE oil and gas India conference and exhibition, Mumbai, Bharat, April 9–11. SPE-194578-MS. https://doi.org/10.2118/194578-ms.
-
Shahbazi K, Zarei AH, Shahbazi A, Tanha AA (2020) Investigation of production depletion rate upshot on the near-wellbore stresses in the two Iranian southwest oilfields. Petr Res 5(4):347–361
-
Sharland R, Brett Davies A, Peter Heward A, Horbury D (2001) Arabian plate sequence stratigraphy. GeoArabia https://www.researchgate.internet/publication/279778628
-
Song I, Haimson BC (1997) Polyaxial strength criteria and their use in estimating in situ stress magnitudes from borehole breakout dimensions. Int J Stone Mech Min Sci 34(3–4):116.e1-116.e16
-
Tan T, Zhang H, Li J, Wang H, Cai Z, Yu Q, Yang Yard, Chen Y, Liu Grand, Deng Q, (2019) Analysis on collapse pressure and fracture pressure of a borehole in natural gas hydrate germination. In: The 53rd U.S. Rock mechanics/geomechanics symposium, New York City, New York
-
Vahrenkamp VC, Laer PV, Franco B, and Celentano MA, (2015) IPTC-18470-MS Late jurassic to cretaceous source rock prone intra-shelf basins of the Eastern Arabian Plate – Interplay between tectonism, global anoxic events and carbonate platform dynamics
-
Van Buchem F, Razin P, Homewood P, Philip J, Eberli Grand, Platel J, Roger J, Eschard R, Desaubliaux 1000, Boisseau TM (1996) High-resolution sequence stratigraphy of the Natih Formation (Cenomanian/Turonian) in Northern Oman distribution of source rocks and reservoir facies. GeoArabia. https://doi.org/ten.2113/geoarabia010165
-
Van Buchem MD, Simmons H, Droste R, Davies Brett (2011) Late aptian to turonian stratigraphy of the eastern Arabian plate - depositional sequences and lithostratigraphic nomenclature. Pet Geosci. https://doi.org/10.1144/1354-079310-061
-
Vernik Fifty, Zoback MD (1992) Interpretation of maximum horizontal master stress magnitude from stress-induced well bore breakouts in the Cajon Pass scientific research borehole. J Geophys Res Solid Earth 97(B4):5109–5119
-
Zhang J (2013) Borehole stability assay accounting for anisotropies in drilling to weak bedding planes. Int J Rock Mech Mining Sci lx:160–170
-
Zoback Physician (2010) Reservoir geomechanics. Cambridge Academy Printing, Cambridge
-
Zoback Doctor (2010) Reservoir geomechanics. Cambridge University Press, Cambridge
-
Zoback Doctor, Barton CA, Brudy M, Castillo D (2003) Determination of stress orientation and magnitude in deep wells. Int J Rock Mech Min Sci forty(seven/viii):1049–1076
Acknowledgements
Thanks are given to anonymous domain experts for their input and insight, without which this inquiry would not have been possible. The second author would like to acknowledge the Research Council of the University of Tehran.
Funding
This research did non receive whatever specific grant from funding agencies in the public, commercial, or not-for-turn a profit sectors.
Author information
Affiliations
Corresponding author
Ethics declarations
Disharmonize of interest
No potential conflict of interest was reported by the writer.
Boosted information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations
Rights and permissions
Open Access This commodity is licensed under a Creative Commons Attribution four.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long every bit you lot give appropriate credit to the original writer(south) and the source, provide a link to the Creative Commons licence, and indicate if changes were fabricated. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended utilise is not permitted by statutory regulation or exceeds the permitted employ, yous will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/past/4.0/.
Reprints and Permissions
Nearly this article
Cite this commodity
Hoseinpour, M., Riahi, K.A. Determination of the mud weight window, optimum drilling trajectory, and wellbore stability using geomechanical parameters in one of the Iranian hydrocarbon reservoirs. J Petrol Explor Prod Technol 12, 63–82 (2022). https://doi.org/x.1007/s13202-021-01399-5
-
Received:
-
Accepted:
-
Published:
-
Issue Engagement:
-
DOI : https://doi.org/x.1007/s13202-021-01399-5
Keywords
- Dynamic modulus
- Maximum horizontal stress
- Mud weight window boundary
- Shear rock failure
- Tensile rock failure
Source: https://link.springer.com/article/10.1007/s13202-021-01399-5
Posted by: ramergoope1995.blogspot.com


0 Response to "How To Draw A Polar Plot For Mud Weight"
Post a Comment